Plugins for Photoshop, Elements, Lightroom, PSP & others
Plugins for Photoshop, Elements, Lightroom, PSP & others
| Mac | PC | |
| Adobe Photoshop 3.0, 4.0 | Adobe Photoshop 3.0.x, 4.0 | |
| Adobe Illustrator 7.0 | Fractal Design Painter 4.0.x 32-bit (no alpha channels) | |
| Macromedia Freehand 7.0 | JASC Paint Shop Pro 4 (32-bit) and 5* | |
| Adobe PhotoDeluxe 2.0 | Adobe Illustrator 7.0 | |
| Macromedia Freehand 7.0 | ||
| ColorWorks 3:Net | ||
| Corel Draw 6, 7
Ulead PhotoImpact 3, 4 |
These programs do not support Filter Factory filters:
| Mac | PC | |
| Adobe Premiere 4.0 (has its own Filter Factory) | Picture Publisher 6, 7 | |
| Macromedia xRes 3 | ||
| PixelPaint Pro 3.0 | ||
| Ray Dream Designer 4.0 | ||
| Debabelizer 1.6.5 | ||
| Deneba Canvas 5.0 |
majordomo@aurdev.com
with the following in the body of the message:
subscribe ff
majordomo@aurdev.com
with
unsubscribe ff
in the body of the message.
The groups rules as of February 1997 are:
To send a filter in, we are suggesting the following format:
r: xxxxxxx
g: xxxxxxx
b: xxxxxxx
a: xxxxxxx
ctl[x]:
val[x]:
2.2.1 Photoshop images (pixels vs. vectors)
If you have never worked with graphic programs before (we doubt it), we will supply you here with information about graphics, pixels, etc. There are two different kinds of graphic programs:
a) Drawing programs
b) Painting programs
Drawing and painting are not synonyms. Drawing programs are vector-oriented programs. Usually you use predefined objects such as lines, circles, rectangles, etc. and combine them on your worksheet (the worksheet's width and height are usually measured in inches or millimeters). You can assign each object an individual color, filling, thickness, etc. This means you can edit each object without losing information, even if the objects are 'hidden' behind others. The good thing about vector-based graphics is that you can scale them into any size you want without losing information like in pixel-based graphics; each object's data is a mathematical information - scaling the picture only rearranges the mathematical information. If you could zoom into these drawings till infinity, you would not notice any jaggies (as aliasing is called). Typical programs are Corel DRAW!, Adobe Illustrator or Macromedia Freehand.
Painting programs are pixel-based programs. Images edited here are usually scanned pictures or painted with different tools. Tools are available to manipulate your image in any way you want. You can use brushes, selections, smudge, eraser, paintbucket, etc. Your image's width and height are always measured in pixels - the painting program helps you by telling you how wide/tall your image will be when printed. Each pixel contains an intensity information and all pixels have the same width/height. Depending on your image the pixels contains grayscale or color information. Another possible information is an alpha value, giving the pixel a transparency option. This is great when compositing two or more images into one (e.g. clipping a person from an image and putting him/her into another background). The difference to the vector-based picture is that once you paint over a pixel, the original pixel information is gone. Scaling an area of an pixel-based image is problematic. Scaling down means that the area width is lessened, thus the new area is composed by less pixels from the original area. Some pixels get lost. Scaling up means that the area width is greatened, thus the new area is composed by more pixels from the original area. New pixels have to be 'invented', in Photoshop this is called interpolation. Typical programs are Adobe Photoshop, Corel Photopaint and Fractal Design Painter.
There are also some graphic programs in the market which can combine vectors and pixels, but we won't be needing information about these. Let's check the paint programs a bit more. As I said, each image is composed by pixels. For example a common image size has a width of 640 pixels and a height of 480 pixels. Normally you say the image is 640x480 pixels big (or small :-)). In order to be able to work with the pixels, you need their adresses. This is solved by a cartesian coordinate system. x will give you the horizontal position and y will give you the vertical position of the pixel. The origin (0/0) of the coordinate system is on the top left of the image. The biggest values for x and y would be in our image (639/479). ??? Did I say 639 and 479? Yes! This is because the origin is also a part of our image, meaning x can have a value from 0, 1, 2, 3, ..., 637, 638, 639 (a *total* of 640 pixels). Another common image size would be 800x600 big and you can address all the pixels between 0/0 and 799/599, inclusive.
By the way, Photoshop (and several other programs) also works with vector-based objects. Huh? Yup, in case you never worked with them, I am talking about paths... (oh, those). Paths can be seen as line objects which can be connected altogether. Ideal for clipping and for effects.
Note 1: For the math wizzes reading this, how many bytes would it take to compose a 640x480 image? Let's see, we have 640 x 480 pixels = 307200 pixels. Each pixel being 1 byte big gives us 307,200 bytes! A Kilobyte is an amount of 1024 bytes. 307,200 / 1024 = 300 KB.
Note 2: Remember watching a B/W TV? Actually, you did not watch black *and* white, you watched black, white *and* the different grays... So you watched grayscale TV!
Now, let's take a colored image. This is a bit more complicated. The
color television, the computer monitor and a scanner work all with RGB.
Red, Green and Blue. Some of you might ask me, "Oh yeah, smarty, well,
what about *YELLOW*???" Thing is that the colors are mixed in an additive
way depending on their wavelength (this works only on ray emitting objects
such as the computer monitor). Look what the mixing of RGB will result
to:
| No Mix: black Red + Green: yellow Red + Blue: magenta Green + Blue: cyan |
 |
There are also following color spaces: CIE Lab, HSB and CMYK.
CMYK ist used in the printing technology, i.e. when you prepare your
image for print. You need the colors Cyan, Magenta, Yellow and Black.
With these colors you can print almost any color you can think of (no,
no gold... :-)). Color is made up of pigment and the pigment reflects
or absorbs light. Because it absorbs certain wavelengths of white light
we talk of subtractive mix:
| No mix: white (in case we're printing on white paper) Cyan + Magenta: violet (Blue) Cyan + Yellow: green Yellow + Magenta: red All Three: theoretically black, but as this mixture gives the image a dirty tone and has not much contrast, black is printed on the image to greaten the contrast |
 |
This is what happens when you click on Filters -> Synthetic...
-> FF:
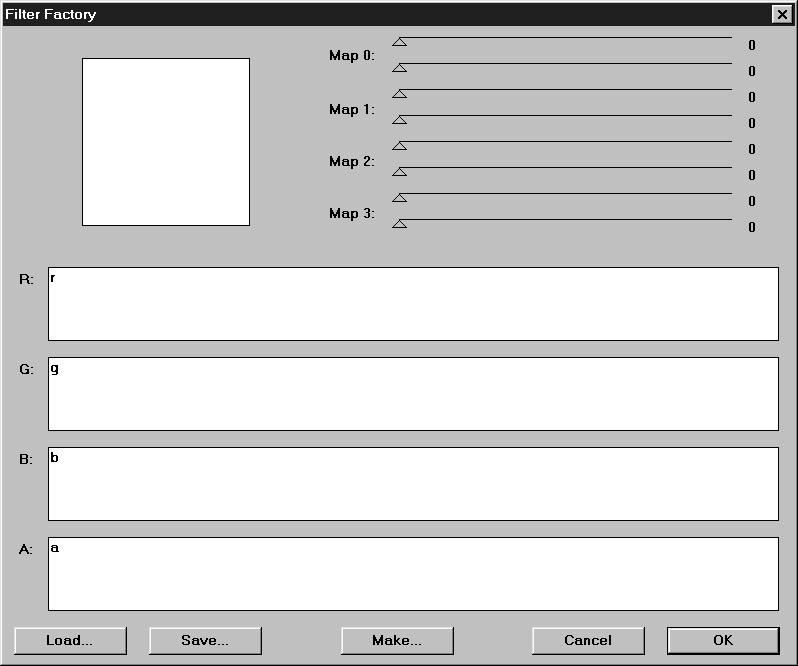
On the upper left side you can see a preview window.
On the upper right side you can see eight sliders.
In the middle there are 3 or 4 coding areas (depending if your image has
transparency; if it doesn't, you are probably working on a background
layer with r,g,b. if it does have transparency you will see r,g,b,a).
This is where you type in your code. Notice that FF already puts on startup
the variables r,g,b (and a) on their respective channel coding areas.
On the bottom you can see buttons (see 2.2.10 Input/Output
for more details).
| r | Returns the red channel value of the current pixel |
| g | Returns the green channel value of the current pixel |
| b | Returns the blue channel value of the current pixel |
| a | Returns the alpha channel value of the current pixel |
| All of the above return a value from 0 to 255 | |
| c | Returns the channel value of the current pixel in the current channel Would be the same as typing either r, g, b or a in their respective coding areas or using src(x,y,z) (see 2.2.6.a) |
| x | Returns the x-coordinate (horizontal position) of the current pixel can be an integer from 0 to X-1 |
| y | Returns the y-coordinate (vertical position) of the current pixel can be an integer from 0 to Y-1 |
| X | Returns the image width X can be an integer from 1 to 30,000 |
| Y | Returns the image height Y can be an integer from 1 to 30,000 |
| i, u, v | Return the i,u,v values of the current pixe in YUV space i can be an integer from 0 to 255 u can be an integer from -56 to 56 v can be an integer from -78 to 78 |
| z | Returns the channel index of the current pixel in the code area can have a value from 0 to 2, depending in which code area this variable is 0 means red, 1 means green, 2 means blue and in your alpha channel you will get 1 |
| Z | Returns the total amount of channels can be an integer either 3 (r,g,b) or 4 (r,g,b,a) |
| d | Returns the angle (direction) of the current pixel from the center
of the image can have an integer from -511 to 512 (see 2.2.6.b Polar coordinates) |
| dmin | Returns 0 |
| D | Returns the total amount of angles within the image is always 1024 |
| m | Returns the magnitude (distance) of the current pixel from the center
of the image can be an integer greater than 0 |
| mmin | Returns 0 |
| M | Returns the total amount of magnitudes in the image is an integer half the diagonal size of the image |
Arithmetic operators:
| + | Adds two numbers, variables,... |
| - | Subtracts second number from the first,... |
| * | Multiplication |
| / | Division |
| % | Modulo When dividing a number from the other, you always have a remainder from 0 upwards. The modulo returns the remainder. For example, 10 % 3 would return 1. |
Logical operators:
| && | Logical AND (between two expressions) returns 1 if both expressions equal 1, else 0 |
| || | Logical OR (between two expressions) returns 1 if one or both expressions equal 1, else 0 |
| ! | Logical NOT (for use with one expression at the right) |
| == | Equals to (between two expressions) |
| != | not equal to (between two expressions) |
| > | greater than (between two expressions) |
| < | < less than (between two expressions) |
| >= | greater than or equal to (between two expressions) |
| <= | less than or equal to (between two expressions) |
Logical operators can be best used with conditional operators
Example: r==5 will return 1 if the red pixel value equals 5, else
will return 0 if the red pixel value does not equal 5
Bitwise logical operators:
| & | bitwise AND (between two expressions) |
| | | bitwise OR (between two expressions) |
| ^ | bitwise XOR (exclusive OR) (between two expressions) |
| ~ | bitwise NOT (before one expression) |
| << | shifts left |
| >> | shifts right |
Conditional operator:
| ?: | question mark and colon |
a) Example: r>120 ? r-50 : r+50
Above example will test the red value of the current pixel if it is greater than 120. If it is, the intensity is lowered (r-50), if the value is less than or equal to 120, the intensity is pushed up by a value of 50.
b) Nesting (Condition in a condition) is allowed
r>120 ? (g<120 ? r+10 : r-10) : (g<120 ? r+20 : r-20)
If the red value of the current pixel is greater than 120, then the green
channel is tested if less than 120. If it is not, then the red value is
lowered by 10. This means that the amount changed in the red channel depends
on the green channel value.
| r> 120 ? | |||
|---|---|---|---|
| Yes | No | ||
| g < 120 ? | g < 120 ? | ||
| Yes | No | Yes | No |
| r + 10 | r - 10 | r + 20 | r - 20 |
(r<120 && x>120) ? 50 : 100 is put in the green coding area
If the red channel value is less than 120 AND the pixel position is greater than 120, then the green channel value is set to 50, otherwise set the green channel value is to 100.
Comma (,) operator
The comma separates two or more algorithms, evaluates both but returns
the last.This is mostly used when working with the get and put functions.
One or more put-functions save the algorithm?s return code into an internal
memory, whereas the get-function load the saved numbers into memory again.
For example, when part of the code is used many times, you can put the
code into memory once and load it with the get function many times.
2.2.6 Functions
This is getting pretty interesting, don't you think? Now it'll get much better and a bit more complicated. If you are a novice to FF, I would advise you to experiment with each function separately in order to fully understand what it does. We will try to explain each function in this section and in the tutorial sections thoroughly, so you can start ex-perimenting without doubts right away. The variables used here are only placeholders, it does not mean that the functions only work with them.
a) Normal functions
| abs(a) | returns the absolute value of a. If a=-50, a value of 50 is returned |
| add(a,b,c) | adds a and b together, compares the result with c and the lesser value is returned |
| cnv(m11,m12,m13, m21,m22,m23,m31, m32,m33,d) |
The convolver is similar to the Custom Filter in Photoshop. Each
pixel and its eight neighbouring pixels are evaluated to get a new
result. The map looks like this: m11 m12 m13
m21 m22 m23 m31 m32 m33
The target pixel is the one in the middle (m22). Each m??-value
is multiplied with the pixels corresponding to the map (this is
called weighting), all values are added together and divided by
d (normally is d the total amount of the weigths). |
| ctl(i) | see 2.2.7 Sliders, returns an integer between 0 and 255 |
| dif(a,b) | subtracts b from a and returns its absolute value |
| get(i), put(v,i) | FF has internally 256 cells, where you can store and request values. put(v,i) will evaluate the expression v and store the result in cell i. get will return the result in cell i. r: put(src(X-x,Y-y,z),0),get(0) As you can see, the image is mirrored horizontally and vertically, whereby the values are taken from the red channel and stored in cell 0. Finally, all code areas request the value of cell 0. Note that your image will turn grayscale (because the red channel values were stored, and the green and blue channel values were ignored). |
| map(i,n) | returns the larger value, either a or b |
| max(a,b) | returns the larger value, either a or b |
| min(a,b) | returns the lesser value, either a or b |
| mix(a,b,n,d) | works like this: a*n/d + b*(d-n)/d The two input values (a,b) are combined with the fraction n/d. If the fraction is close to 0, b is returned. If the fraction is close to 1, a is returned. If the fraction is close to 1/2, the average of a and b is returned |
| rnd(a,b) | returns a random number between a and b, where a < b |
| scl(a,il,ih,ol,oh) | the scale function maps the value a from an input range (il, ih)
to an output range (ol,oh) scl(r,0,255,100,200) will evaluate the red channel value of the current pixel. According to the scale function, values near 0 will become 100 and values near 255 will become 200. Respectively, a value of 128 will turn into 150. |
| sqr(x) | returns the square root of x |
| src(x,y,z) | returns the channel pixel value in coordinates x,y in channel z,
whereby the return value equals an integer between 0 and 255 src(400,200,c) will return the pixel value at 400/200 in the current channel and src(x,y,z) equals the variable c (see 2.2.4) |
| sub(a,b,c) | difference between a and b (absolute value), compares the result with c and the greater value is returned |
| val(i,a,b) | see 2.2.7 Sliders, returns an integer between a and b |
Before explaining the functions, you should have some knowledge on polar
coordinates.
As you know, cartesian coordinates have the origin on the top-leftmost
pixel of our image (0,0). The origin of polar coordinates is in the center
of the image (X/2, Y/2).
Cartesian coordinates are defined by a horizontal position (x) and a vertical
position (y). Polar coordinates are defined by an angle (d for direction)
and a magnitude (m) (radius or distance from the origin, i.e. from the
image's center). 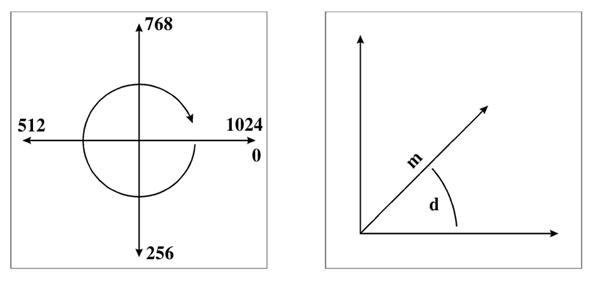
Notice that the angle d can be any positive or negative integer (0 inclusive). A value of 1024 means a full rotation, while multiples of 1024 (2048, 3072, 4096, etc) mean multiple rotations. The magnitude m can be an integer from 0 to M (half the diagonal image size). There are ways to convert cartesian into polar coordiantes and vice-versa.
Cartesian-polar conversion:
This means we have the x and y coordinates and convert them to d and m,
i.e. horizontal/vertical to direction/magnitude conversion. Let's say
we have the coordinates (3/4). Let's make a pythagoran triangle from the
origin: We move from (0/0) to (3/0) to (3/4). The magnitude (distance)
of the pixel from the origin is represented by the triangle side (hypotenuse)
(0/0) to (3/4). Direction is the angle of this line to the x-axis (horizontal
axis). The length of the hypotenuse (distance or magnitude) is the square
root of the addition of x squared and y squared. The angle (direction)
is the arctan when dividing y by x. This means our distance is 5 and the
angle 53,13°.
Polar-cartesian conversion:
Now we have d and m and want to convert these to x and y. Let's say, we
have the magnitude (distance) 5 and the angle (direction) 233,13°.
The cosine of the angle is the division of the x-length by the magnitude.
In order to get x, we multiply the cosine of the angle with the magnitude.
The sine of the angle is the division of the y-length by the magnitude.
In order to get y, we multiply the sine of the angle with the magnitude.
This means x is (5 * cos(233,13))= -3 and y is (5*sin(233,13°))= -4.
Our pixel's coordinate is thus (-3/-4).
| c2d(x,y) | This returns the direction (angle) of the pixel at (x/y) from (0/0). Mathematically, this is the arctan after dividing y by x. Values returned are integers from -512 to 512. |
| c2m(x,y) | Returns the magnitude (distance) of the pixel at (x/y) from (0/0). Mathematically, this adds the squared values of x and y and returns the square root. The values returned are integers from 0 to M*2. |
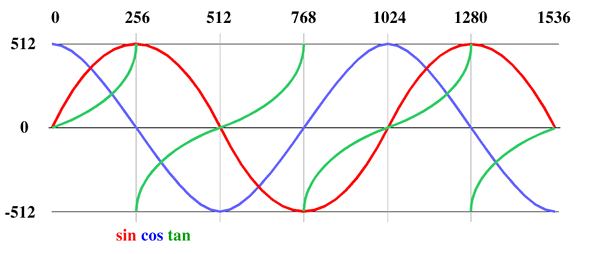
| cos(x) | Remember trigonometry and terms like amplitude and wavelength? Let's picture a full wavelength from 0 to 1024. The value returned is an integer between -512 and 512, Macintosh FF returns an integer between -1024 and 1024. Cos(0) returns a full amplitude (512), while cos(256) returns 0, cos(512) returns -512 , cos(768) returns 0 again and cos(1024) returns 512. Values greater than 1024 restart the cosine wave. |
| r2x(d,m) | This returns the x-coordinate at a polar coordinate (d/m). |
| r2y(d,m) | This returns the y-coordinate at a polar coordinate (d/m). |
| rad(d,m,z) | This function resembles the src(x,y,z)-function in cartesian coordinates. rad(d,m,z) returns the pixel value m pixels at an angle (direction) of d from the origin. Using rad(d,m,z) is the same as using src(x,y,z) or simply c. |
| sin(x) | Works the same as cos(x), returns an integer between -512 and 512, Macintosh FF returns an integer between -1024 and 1024. Sin(0) returns 0, sin(256) returns 512, sin(512) returns 0, sin(768) returns -512 and sin(1024) returns 0. |
| tan(x) | Works almost like cos(x) and sin(x), returning an integer between -512 and 512, Macintosh FF returns an integer between -1024 and 1024 (instead of going to infinity :-)). tan(0) returns 0, tan(256) returns 512, *tan(257) returns -512*, tan(512) returns 0, starting all over again. |
Now you might say, having slider values between 0 and 255 won't be helping you much. Maybe you'll need more values or less. No problem, with the val(i,a,b) function, you can give the slider i the range from a to b (b can be lesser than a). Note that ctl(i) and val(i,a,b) are two different functions which returns ranges from a slider.
ctl(2) will return an integer from 0 to 255, depending on the slider
2 setting
val(2,-128,128) will return an integer from -128 to 128.
When creating the filter (with a val(2,-128,128)) with Make... you'll
be pretty shaken because when the user accesses the filter, all slider
values still range optically from 0 to 255, although internally, slider
2 *will* return a number between -128 and 128. You might say you're not
WYSIWYGing (What You See Is What You Get) :-( Let's hope future versions
of FF will relieve us this pain.
2.2.8 What's that darn yellow caution sign? (Duh)
While typing in the code, you might encounter a yellow caution sign appearing and disappearing. This sign tells you simply that the code you typed as of your last keypress has a syntax error. Either you have a typo in your code or your code cannot be used like you wanted it to work. Check out the parenthesises, the commas, the upper- or lowercase functions/variables.
Pressing CTRL-Z (PC) will undo your last typing in the boxes. Pressing TAB will get you in the next text box. You can cut and paste text to and from the clipboard using shift-delete and shift-insert ( CTRL-C and CTRL-V work too).
You might also encounter that your code is correctly typed, but your
filter does not give you the results you expected. Check the values you
are giving to your code, for example ctl(20) won't help much, because
there is no slider 21 (you have just got eight, isn't that enough? :-)).
Image Types
Filter Factory works only with RGB files. In RGB it only works if all 3 channels (or 4 including Alpha) are activated. This is not completely true anymore as it is possible to hack FF so it will work in all modes.
Memory Problems
Filter Factory is a very memory-hungry program. To make it worse - it can only make use of physical memory. So even if you have 1GB of virtual memory it doesn't help if the image you want to filter is bigger than about 50% of your available RAM. So if you have a memory problem make sure that the clipboard is empty, no snapshot is in memory and no other images are opened, then perhaps you have a chance. Or you try to do it in two or more selections.
Precision
Filter Factory calculates with integer mathematics. Probably this speeds everything up, on the other hand it has some side effects. Especially on filters that use circles or sine-functions you will discover those wonderful stairs that give you the jaggy look (also called aliasing). Sorry, there is no way to solve this problem other than to apply a blur after applying the FF filter.
Sliders
The sliders do always show values between 0 and 255, no matter what the filter needs it for. So even if you need something like -180 to 180 it shows 0 to 255. Also, the resolution is never higher than 256 steps.
Random Function
This one is not very random. Actually it uses a lookup table that is always the same. So if you produce two layers of noise and overlay them with the difference mode you'll see black. A better method to get random numbers is to use pixel values from the image itself, but this works only as long as the image isn't too simple. Example: src(scl(r,0,255,0,X),scl(g,0,255,0,Y),b%2)
From Joe Ternasky's keyboard:
"The Factory limits the length of the expressions to 1K each, for no really good reason. Programmers just love powers of two, and I'm no exception. It also places limits on the length of the generated code. These limits are different for different processor architectures (68000, PowerPC and 80x86). You're running up against the generated code limit, again for no really good reason.
One way around this is to eliminate common sub-expressions (via the
get/put functions and the comma operator) or to move part of your expression
into the alpha field. In either case, if you can evaluate part of the
expression separately then this intermediate value can be placed into
an anonymous variable (via put) and then read back where it's needed (via
get). Anything else that you can do to simplify the expressions would
also help, but you've probably already tried that."
Preview
The preview window, also called proxy, (see image page 8) varies its size on Windows and Mac versions, so when creating codes you will be seeing effects which look okay in the preview but have a different effect in the large image. You can correct this by using the X and Y variables (see tutorial section 2.3.4 Code optimization).
2.2.10.2 Loading the code
Loading the code is easier. Simply press the Load... button and look
in the directory where you saved or copied the .AFS file(s), load it and
now you're on your own...
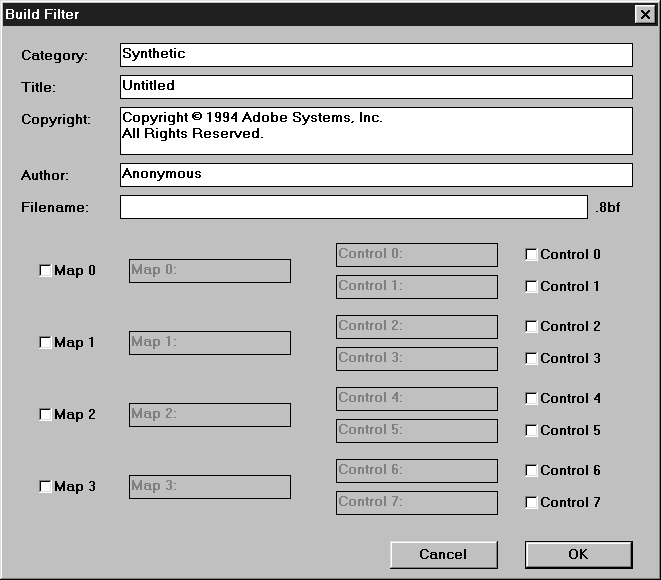
Category is what you first see when you click on the filter menu. It can be a completely new name, a name where you can relate it to (blur filter, stylize, whatever...) or the name suggested by the author who created the filter.
Title is the actual name of the filter. Give a name that will tell a Photoshop-newbie right away what it does. Or use the name the author suggests.
Copyright is obvious. Type the copyright (if you are the author) or type the one suggested by the author.
Filename is the name of the plug-in. Just type the name, not the extension (on the right side of the edit window you can see '.8bf'. FF automatically creates an .8bf-filter (you just have to supply it with a name) and saves it in your plug-in directory. In the Mac version of FF it will ask you the folder where you want to save the plugin.
If the filter you are creating uses sliders or maps, you have to check the map or slider number. After checking the checkbutton you can assign a name to it. Use a name that will tell the user what the map or slider does (e.g. 'radius', 'line color', 'amplitude', ...). Notice you can't assign Map 0 *and* slider(s) 0 or/and 1. This is because the map works with the slider values. You can assign Map 0 and a slider>1.
Now all you can do is press either Cancel or OK. Pressing OK will create the plug-in and save it in your plug-in directory. You must however, exit Photoshop and restart it in order for it to recognize the new plug-in(s).
Note: You might encounter some problems when trying to access a filter. This might happen if you did not assign the a channel a value. Always remember to include the a: (alpha channel) code. If the plug-in doesn't care about transparency in your images, use the code:
a: a in your alpha channel.
FFDECOMP.EXE is a MS-DOS utility which will deconvert a .8bf into a .afs and into a .txt file. You can find it at: http://http://johann.simplenet.com
The second program is called Plug-In Manager for Adobe Photoshop. If your Photoshop has problems with the thousands of filters you have in your plug-in directory/folder, then this could be the solution. You can turn on/off filters individually, move them to other categories and it will also deconvert plug-ins created by Filter Factory. You can find it at: http://johann.simplenet.com
An alternative is Harry's Plugin Commander (PiCo), which converts
various FF related formats like .afs, .8bf, .pff, .prm, .ffl and .txt.
PiCo also includes a Editor to create FF plugs, an Archiver that archives
e.g. 1000 Filters in a 512K small file and you can even change the categories
of non-FF Photoshop plugs.You can download it at: http://www.fortunecity.com/lavendar/kane/39/
r: 255-r
g: 255-g
b: 255-b
a: a
we could also use:
r,g,b: 255-c
a: a
r,g,b: src(X-x-1,y,z)
a: a
r,g,b: src(x,Y-y-1,z)
a: a
r,g,b: src(y,X-x-1,z)
a: a
r,g,b: src(Y-y-1,x,z)
a: a
r,g,b: src(X-x-1,Y-y-1,z)
a: a
r: put((76*r+150*g+29*b)/256,0),get(0)
g,b: get(0)
a: a
or simply:
r,g,b: i
a: a
TUTORIAL A: Creating blends
a) Linear blends
Please work with a 512x512 RGB picture for this tutorial.
When examining our pixel values in a blend, we see that the values are
consecutive. Let's say, we have a grayscale image and we want a horizontal
blend from black (0) to white (255). We could use the pixel positions
(x,y) in order to create a pixel value for a blend. Let's create a black
to white blend in an RGB image:
r,g,b: x
Yes, that's it. Problem is, if our image or selection width is greater or less than 256, then we would get a not quite complete blend. So, we need also the image's width information (X). In order to create a smooth blend from left to right in any image, we would use this code:
r,g,b: x*255/X
or
r,g,b: scl(x,0,X-1,0,255)
Now, let's say we need multiple blends. A way to do it is with the MODULO operator. Try this:
r,g,b: x%256
While the pixel position rises, we get consecutive numbers... 0, 1, 2, 3, ....254, 255, and now it starts all over again... 0, 1, 2, 3, 4, 5... Thus, we have two (512/256) black to white blends in our image. Do you need more blends? No problem.
r,g,b: x%128*2
Now we have four blends (512/128), but because the maximum value the modulo operator can return is 127, we have to multiply it with 2 (127*2=254), so we can see a nice contrast blend. You could use also following code:
r,g,b: scl(x%128,0,127,0,255)
If you watch the maths while doubling the amount of blends, you would get following "law":
x % (256 / no of blends ) * no of blends
The code for it with slider 0, where we control the amount of blends:
r,g,b: x%(256/ctl(0))*ctl(0)
Nice, huh? Now, if you want - with one filter - be able to create either horizontal or vertical blends, use slider 1 to control the blend movement:
r,g,b: ctl(1)<127 ? x%(256/ctl(0))*ctl(0) : y%(256/ctl(0))*ctl(0)
Problem is, the amount of blends is not the value selected in slider 0. Now we also need the image's width (X). Remember we used following code for a blend in an image any size?
x*256/X
Now we want two blends. If we multiplied the code with 2 (result would be a value from 0 to 512) and use here our modulo operator (so we can have blends from 0 to 255):
r,g,b: (x * 512 / X) % 256
If we want four blends, we'd need following code:
r,g,b: (x * 1024 / X) % 256
Check out the math law for use with a slider, so the user can input his desired number of blends:
r,g,b: (x * 256 * ctl(0) / X ) % 256
If you want white-black blends instead of black-white, use:
r,g,b: 255-(x*256*ctl(0)/X)%256
Again, if you need the possibility of selecting either horizontal or vertical blends, use slider 1, too:
r,g,b: ctl(1)<127 ? (x * 256 * ctl(0) / X ) % 256 : (y * 256 * ctl(0) / Y ) % 256
ctl(0) exact amount of blends
ctl(1) horizontal/vertical blending
This one combines everything together:
Name: Blender (V/H)
r,g,b:
(ctl(1)<127)?
(ctl(2)<127?(x*ctl(0)*256/X)%256:255-(x*ctl(0)*256/X)%256):
(ctl(2)<127?(y*ctl(0)*256/Y)%256:255-(y*ctl(0)*256/Y)%256)
ctl(0) exact amount of blends
ctl(1) horizontal/vertical blending
ctl(2) black-white / white-black blending
It's pretty ok with this blending and stuff, but they are all black & white..."I need color!!!". Well, all right. We can dispose now of the black-white / white-black blending method, leaving a black-white blending only:
r,g,b: ctl(1) < 127 ? (x*ctl(0)*256/X)%256 : (y*ctl(0)*256/Y)%256
ctl(0) exact amount of blends
ctl(1) horizontal/vertical blending
We will use the 6 available sliders for our blend coloring. In order to do that, we will use the scl(a,il,ih,ol,oh)-function. We know that the resulting values are integers between 0 (il) and 255 (ih). If you examine the red channel code, you'll see that the lowest value is turned into the slider 2 value and the highest value is turned into the slider 3 value.
Category: Neology
Title: HV-Blender
Copyright: (c) 1996 by Werner D. Streidt
100526.16@compuserve.com
Author: Werner D. Streidt
Filename: nhvblend.8bf
r: scl(ctl(1)<127?(x*ctl(0)*256/X)%256:(y*ctl(0)*256/Y)%256),0,255,ctl(2),ctl(3))
g: scl(ctl(1)<127?(x*ctl(0)*256/X)%256:(y*ctl(0)*256/Y)%256),0,255,ctl(4),ctl(5))
b: scl(ctl(1)<127?(x*ctl(0)*256/X)%256:(y*ctl(0)*256/Y)%256),0,255,ctl(6),ctl(7))
a: a
ctl(0) No. of blends
ctl(1) horizontal / vertical blending
ctl(2) red amount of starting blend value
ctl(3) red amount of ending blend value
ctl(4) green amount of starting blend value
ctl(5) green amount of ending blend value
ctl(6) blue amount of starting blend value
ctl(7) blue amount of ending blend value
Pretty neat, you think? Well, we can do another kind of blending...
b) Radial blending
How do we do that? Remember there is a variable called magnitude m (or distance from the image/selection center)? Use again here a 512 x 512 RGB pic.
r,g,b: m
This will give us a radial blend from innerly black to outter white. Let's use multiple blends with m % 256 , but as we can't see much, let's give it more blends:
r,g,b: m * 8 % 256
And because it's so cool using sliders for blend amount and coloring, let's jump right into it (you should know why after the linear blending tutorial):
Category: Neology
Title: Rad-Blender
Copyright: (c) 1996 by Werner D. Streidt
100526.16@compuserve.com
Author: Werner D. Streidt
Filename: nrdblend.8bf
r: scl(m*ctl(0)%256,0,255,ctl(2),ctl(3))
g: scl(m*ctl(0)%256,0,255,ctl(4),ctl(5))
b: scl(m*ctl(0)%256,0,255,ctl(6),ctl(7))
a: a
ctl(0) Blend amount
ctl(2) red amount of starting blend value
ctl(3) red amount of ending blend value
ctl(4) green amount of starting blend value
ctl(5) green amount of ending blend value
ctl(6) blue amount of starting blend value
ctl(7) blue amount of ending blend value
c) Rotational blending
To have the blends rotate around the center like a helicopter propeller, we have to work with the angle (direction) d. Problem is, d returns values from -512 to 512, so we can scale it from 0 to 1024. Then we use our modulo %256 and finished.
r,g,b: scl(d,-512,512,0,1024) % 256
To make a user controlled amount of blends, we'll have to change the last term in the scl function. The above function gives us four blends. So, it should read as follows:
r,g,b: scl(d,-512,512,0,ctl(0)*256)%256
And because it' so nice using sliders for blend amount and coloring...
Category: Neology
Title: Rot-Blender
Copyright: (c) 1996 by Werner D. Streidt
100526.16@compuserve.com
Author: Werner D. Streidt
Filename: nrtblend.8bf
r: scl(scl(d,-512,512,0,ctl(0)*256)%256,0,255,ctl(2),ctl(3))
g: scl(scl(d,-512,512,0,ctl(0)*256)%256,0,255,ctl(4),ctl(5))
b: scl(scl(d,-512,512,0,ctl(0)*256)%256,0,255,ctl(6),ctl(7))
a: a
ctl(0) Blend amount
ctl(2) red amount of starting blend value
ctl(3) red amount of ending blend value
ctl(4) green amount of starting blend value
ctl(5) green amount of ending blend value
ctl(6) blue amount of starting blend value
ctl(7) blue amount of ending blend value
TUTORIAL B: Creating checkered tiling
Did you always want to create a checkered tiling in Photoshop. Yes, there are ways, but too complicated. I'll show you how to create them with a filter.
Let's take a 2 x 2 field (10 x 10 pixels). It would look like this:

We have two different fields: A white one and a black one. The first line (y=0) gives us 255 (white) for the first 5 pixels (0 <= x < 5) and 0 (black) for the last 5 pixels (4 < x < 10). The modulo function returns with x % 10 in a large image and according to the pixel positions, the values 0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0,1,2,3,....
Now, we have to check if we're filling the pixels with white or black. This can be done with the following code:
r,g,b: (x % 10) < 5 ? 0 : 255
I can also work with boolean maths. If I simply use
(x % 10) < 5
then FF would return a 1 if true or 0 as false. Multiplying it with 255 would return values either 0 or 255:
((x%10) < 5 ) * 255
Ok, what's with y? The same code idea:
(y % 10) < 5
How to combine both? We could use the exclusive OR (XOR) idea:
| x < 5 | x> 4 | |
|---|---|---|
| y < 5 | 0 | 1 |
| y> 4 | 1 | 0 |
((x % 10) < 5 ) ^ ((y % 10 ) < 5 )
Now the whole thing multiplied with 255 returns the values 0 or 255:
(((x % 10) < 5 ) ^ ((y % 10 ) < 5 )) * 255
That's a boy... Problem is, the first checker cell is black and not white. There are two possible solutions for this. The easy one:
(((x % 10)> 4 ) ^ ((y % 10 ) < 5 )) * 255
and the boolean one:
(!((x % 10) < 5 ) ^ ((y % 10 ) < 5 ))* 255
Phew, that's it! Adding sliders is another challenge:
a) Sliders represent pixel values
Let's say that with the sliders, we tell FF how thick each checker cell (in pixels) is. As you noticed from the code:
((x % 10) < 5 )
the first number represents the width of two cells and the second number the width of one cell. Thus, our code with a slider would look like this:
(!((x %( ctl(0)*2)) < ctl(0) ) ^ ((y % (ctl(0)*2) ) < ctl(0) ))* 255
Note: There is a radial kind of checker tiling you should try:
(!((m %( ctl(0)*2)) < ctl(0) ) ^ (((d+512) % (ctl(0)*2) ) < ctl(0)
))* 255

b) Sliders represents the total amount of cells in a row/column
This one's a bit tougher. The slider setting has to be converted into a cell width/height. Thus, dividing the width (X) of the image with the cell amount (ctl(0)) would be the following code: X/ctl(0). Let's say the image is 512 pixels wide and we have a slider setting of 8. X / ctl(0) = 512 / 8 = 64. The cell is 64 pixels wide. The complete code would be:
Category: Neology
Title: Checkered Tiling
Copyright: (c) 1996 by Werner D. Streidt
100526.16@compuserve.com
Author: Werner D. Streidt
Filename: nchecker.8bf
r,g,b: (!((x %( X/ctl(0)*2)) < (X/ctl(0))) ^ ((y % (Y/ctl(0)*2) )
< (Y/ctl(0))))* 255
a: a
ctl(0) Cell amount in a row/column
Note: You'll notice that you'll get in some occasions cell parts which
don't belong there. This is due to the fact that the image's width and/or
height is not a multiple of the slider setting. To visualize this problem
create a new RGB image (500 x 500) and another RGB image (512 x 512) and
use the filter with a setting of 8. The problematic image is the 500 x
500, because 500 divided by 8 results into 62,5.
The blenders you learned above are quite nice, you say. Well if you haven't tried it yet, load an RGB-image, create a new layer, create some blends with above filters from 2.3.2. and use multiply to combine your image with the blends. Instead of doing that, I'll show you how to do it much better. I showed you in 2.3.1 how to simulate Photoshop functions/calculations. Let's take the multiply calculation:
(x * y ) / 256
x and y are not the coordinates, but represent a pixel of two equal sized images. Let's see this in two grayscale images. In image 1, pixel at (100/100) has a value of 255 (white) and in image 2, the pixel on the same coordinate (100/100) has a value of 100. Calculating with multiply would result into (255 * 100) / 256 = 99,6 or 99.
Let's take the following code:
r,g,b: ctl(1)<127 ? (x * 256 * ctl(0) / X ) % 256 : (y * 256 * ctl(0) / Y ) % 256
ctl(0) exact amount of blends
ctl(1) horizontal/vertical blending
Remember, we are creating a certain amount horizontal or vertical blends, overwriting the image's data. Now let's combine the code with our image:
code * channel value / 256
r,g,b: (ctl(1)<127?(x*256*ctl(0)/X)%256:(y*256*ctl(0)/Y)%256)*c/256
a: a
Yes, that's it! Now try using the other blending and tiling methods and
experiment with other calculations.
TUTORIAL B: Adding borders to your images
There are different possibilites of creating interesting borders in your images. Let's start very simple with a black border in the 5 outmost pixels. Since we have four borders, we have to check FF's position while scanning the image:
r,g,b: (x<5 || x>X-6 || y<5 || y>Y-6 ) ? 0 : c
The code would say: IF we are on a x-position less than 5 (0, 1, 2, 3, 4) OR on a x-position greater than X-6 (in an 20x30 image greater than 14: 15, 16, 17, 18, 19) OR on a y-position less than 5 OR on a y-position greater than 24 (Y-6) THEN fill these pixels with black (0) ELSE use the original pixel value (c).
Let's add a slider for the border thickness (notice that the parenthesis before the question mark aren't needed; this is because all || (OR) are of higher priority than the ?):
r,g,b: x<ctl(0) || x>X-1-ctl(0) || y<ctl(0) || y>Y-ctl(0)-1 ? 0
: c
ctl(0): Border thickness (in pixels)
An interesting feature would be to invert the border and reuse the filter with different border thicknesses. The code to invert the border would look like this:
r,g,b: x<ctl(0) || x>X-1-ctl(0) || y<ctl(0) || y>Y-ctl(0)-1 ? 255-c : c
Ok, back to our original code. Black is nice but boring, users want colors, so sliders are needed:
r,g,b: x<ctl(0) || x>X-1-ctl(0) || y<ctl(0) || y>Y-ctl(0)-1 ? ctl(z+1)
: c
ctl(0): Border thickness (in pixels)
ctl(1): Red value for border
ctl(2): Green value for border
ctl(3): Blue value for border
Notice how I used ctl(z+1)? The slider value depends on the channel value.
TUTORIAL C: Cutting around
Do you know the Cutout Filter from Alien Skin? Well I created a cutout filter for the poor Photoshopper :-). The idea is to create a shadow on the left and top of the image or selection and move the image data (in the selection) by a certain amount of pixels. The effect would be like having two equal images, one above the other, while the top one has a cut out area, so you can view the bottom image.
To be able to do this, I have to apply four different codes, depending on:
a) am I applying the left shadow
b) am I applying the top shadow
c) am I applying no shadow
d) am I applying both shadows (top + left)
And on all of them, I am moving the pixels by a slider value, which is automatically my shadow amount.
To make things easier, my shadow is 10 pixels wide/high. The first thing I do is to test if I am on section c) (apply no shadow):
(x>9 && y>9) ? c : (cont)
If I am, use the current pixel value, or ELSE... Now I'd like to test if I am on section a) (apply the left shadow):
(x<10 && y>9 ) ? ... : (cont)
If I am, I would have to use with the 'multiply' idea (see section 2.3.1): multiply the blend with the pixel information and divide by 255. Because my x value depends only from values between 0 and 9 inclusive, I have to use the scale function:
scl(x,0,9,100,255) * c/255
The above code will create a 10 pixel wide blend from 100 to 255 in the first ten pixels while using image data as well. So my complete code for section a) looks like this:
(x<10 && y>9 ) ? scl(x,0,9,100,255) * c/255 : (cont)
Now let's check section b) (apply the top shadow), which is the same as a), only with the y coordinates:
(x>9 && y<10) ? scl(y,0,9,100,255) * c/255 : (cont)
The last part (section d) apply both shadows) has to combine both shadow
blends and the image data under it. On a 5 x 5 blend, the top-left part
should look like this (without multiplying it to the image data):
| 0 | 0 | 0 | 0 | 0 |
| 0 | 64 | 64 | 64 | 64 |
| 0 | 64 | 128 | 128 | 128 |
| 0 | 64 | 128 | 196 | 196 |
| 0 | 64 | 128 | 196 | 255 |
min(scl(x,0,9,100,255),scl(y,0,9,100,255))
Combined with the image data:
min(scl(x,0,9,100,255),scl(y,0,9,100,255))*c/255
Now we got all parts, all we have to do is combine them all in one code:
(x>9 && y>9) ? c :
(x<10 && y>9 ) ? scl(x,0,9,100,255) * c/255 :
(x>9 && y<10 ) ? scl(y,0,9,100,255) * c/255 :
min(scl(x,0,9,100,255),scl(y,0,9,100,255))*c/255
Now, that was cool, huh? You ask me why I use a blend from 100 to 255. If you use 0 instead of 100, you'll get a strong shadow. If you use a greater number than 100, the shadow is a bit softer. (You could let the user manipulate it with a slider) All we need now is to add the slider to specify the shadow's width, which will also offset the image or selection by the specified amount. The code to offset the image data would be to change all c variables (using c is the same as using src(x,y,z)) to src(x-ctl(0),y-ctl(0),z).
Ok, here's the complete code:
r,g,b: (x>ctl(0)-1 && y>ctl(0)-1) ? src(x-ctl(0),y-ctl(0),z) :
(x<ctl(0) && y>ctl(0)-1 ) ? scl(x,0,ctl(0)-1,100,255) * src(x-ctl(0),y-ctl(0),z)/255
:
(x>ctl(0)-1 && y<ctl(0) ) ? scl(y,0,ctl(0)-1,100,255) * src(x-ctl(0),y-ctl(0),z)/255
:
min(scl(x,0,ctl(0)-1,100,255),scl(y,0,ctl(0)-1,100,255))*src(x-ctl(0),y-ctl(0),z)/255
a: a
Neology
Shadowcaster 1
ctl(0) Shadow width
You can now change the blending if you like and for each color:
Category: Neology
Title: Shadowcaster
Copyright: (c) 1997 by Werner D. Streidt
100526.16@compuserve.com
Author: Werner D. Streidt
Filename: nshadow.8bf
r: (x>ctl(0)-1 && y>ctl(0)-1) ? src(x-ctl(0),y-ctl(0),z) :
(x<ctl(0) && y>ctl(0)-1 ) ? scl(x,0,ctl(0)-1,ctl(1),255) * src(x-ctl(0),y-ctl(0),z)/255
:
(x>ctl(0)-1 && y<ctl(0) ) ? scl(y,0,ctl(0)-1,ctl(1),255) * src(x-ctl(0),y-ctl(0),z)/255
:
min(scl(x,0,ctl(0)-1,ctl(1),255),scl(y,0,ctl(0)-1,ctl(1),255))*src(x-ctl(0),y-ctl(0),z)/255
g: (x>ctl(0)-1 && y>ctl(0)-1) ? src(x-ctl(0),y-ctl(0),z) :
(x<ctl(0) && y>ctl(0)-1 ) ? scl(x,0,ctl(0)-1,ctl(2),255) * src(x-ctl(0),y-ctl(0),z)/255
:
(x>ctl(0)-1 && y<ctl(0) ) ? scl(y,0,ctl(0)-1,ctl(2),255) * src(x-ctl(0),y-ctl(0),z)/255
:
min(scl(x,0,ctl(0)-1,ctl(2),255),scl(y,0,ctl(0)-1,ctl(2),255))*src(x-ctl(0),y-ctl(0),z)/255
b: (x>ctl(0)-1 && y>ctl(0)-1) ? src(x-ctl(0),y-ctl(0),z) :
(x<ctl(0) && y>ctl(0)-1 ) ? scl(x,0,ctl(0)-1,ctl(3),255) * src(x-ctl(0),y-ctl(0),z)/255
:
(x>ctl(0)-1 && y<ctl(0) ) ? scl(y,0,ctl(0)-1,ctl(3),255) * src(x-ctl(0),y-ctl(0),z)/255
:
min(scl(x,0,ctl(0)-1,ctl(3),255),scl(y,0,ctl(0)-1,ctl(3),255))*src(x-ctl(0),y-ctl(0),z)/255
a: a
ctl(0) Shadow width
ctl(1) Red intensity
ctl(2) Green intensity
ctl(3) Blue intensity
Now, had I given you the above code, could you decode it back to know
what it actually does? I think with lots of time and good decoding tactics.
I also have problems when trying to decode available codes!
TUTORIAL D: Mosaic Filter
This would normally go into "Simulating program solutions", but there are some new features included. This tutorial is a modified email to the Discussion Group by Ilya Razmanov about mosaics.
For this we need the MODULO function (see, this MODULO is getting quite popular in image synthesis!) and the source function:
r,g,b: src(x-x%10,y-y%10,z)
a: a
Above code would result into blocks of ten pixels width and height. The source is always the pixel in the top-left corner. While we are moving further from it away, the modulo helps us getting the first pixel (in the 10 x 10 block) as source.
Now, we want to give the user more freedom with block size, let's add a slider:
r,g,b: src(x-x%ctl(0),y-y%ctl(0),z)
a: a
Of course, you could use another slider for the block height.
Let's say we want to add a border around each block. We would have to check if a certain value is reached according to x and y position and Modulo:
r,g,b: (x%ctl(0)==0 || y%ctl(0)==0) ? 0: src(x-x%ctl(0),y-y%ctl(0),z)
a: a
A nice feature would be adding a border color with slider values (changing the 0 with ctl(z+1)):
r,g,b: (x%ctl(0)==0 || y%ctl(0)==0) ? ctl(z+1): src(x-x%ctl(0),y-y%ctl(0),z)
a: a
ctl(0) mosaic block size
ctl(1) border color (red)
ctl(2) border color (green)
ctl(3) border color (blue)
TUTORIAL E: Weaving the image
Weaving a picture is not so complex as it sounds. A weave pattern is a neverending pattern on the image, so we can work on its smallest possible area, an 2 x 2 area.
+-----+-----+
| A | B |
+-----+-----+
| C | D |
+-----+-----+
The tiles A and D are equal, in them we create a vertical black-white-black blend. Tiles B and C are a horizontal black-white-black blend. Let's say each tile is 8 pixels wide and 8 pixels high, giving us a rendering area of 16 x 16. First, I want to check if FF is in area A or D. This is done with
(x<8 && y<8) || (x>7 && y>7)
I will have to create a vertical black-white-black blend into the areas A and D, so because it is composed by two blends (black to white and white to black), I'll have to check again if I am already passing half the tile height, in our case the tile height equals 8. The blend is created with the modulo operator. The highest value in our case a 4, so in order to get a good blend from black to white, we have to multiply it with 64; 64 * 4 = 256:
y%8 < 4 ? (y%8+1)*64 : (8-y%8)*64
The first modulo operator returns 1, 2, 3 and 4, then multiplying it with 64. the second modulo operator returns after being subtracted with 8 the values 4, 3, 2 and 1, then multiplied with 64. In both cases, FF returns us the values 64, 128, 192, and 255. The same is done with the horizontal values. So, we first check if we are dealing with areas A and D and apply the vertical blending if necesary, otherwise the horizontal blending is applied.
I have also included two put-functions, to keep the values in two cells in memory.
R:
put(x%16,0), put(y%16,1),
(get(0)<8 && get(1)<8) || (get(0)>7 && get(1)>7)?
(y%8)<4?(y%8+1)*64:(8-y%8)*64:
(x%8)<4?(x%8+1)*64:(8-x%8)*64
G,B:
(get(0)<8 && get(1)<8) || (get(0)>7 && get(1)>7)?
(y%8)<4?(y%8+1)*64:(8-y%8)*64:
(x%8)<4?(x%8+1)*64:(8-x%8)*64
A: 255
Let's take a slider to tell FF which tile size we want. We have to change all numerical values above with a slider value. In above example, the tile size was 8 x 8. Every 8 is changed to ctl(0), every 7 to (ctl(0)-1), 16 into (ctl(0)*2) and 64 into (256*2/ctl(0)).
So, the code will look like this:
R:
put(x%(ctl(0)*2),0), put(y%(ctl(0)*2),1),
(get(0)<ctl(0) && get(1)<ctl(0)) || (get(0)>(ctl(0)-1)&&get(1)>(ctl(0)-1))?
(y%ctl(0))<(ctl(0)/2)?(y%ctl(0)+1)*(256*2/ctl(0)):(ctl(0)-y%ctl(0))*(256*2/ctl(0)):
(x%ctl(0))<(ctl(0)/2)?(x%ctl(0)+1)*(256*2/ctl(0)):(ctl(0)-x%ctl(0))*(256*2/ctl(0))
G,B:
(get(0)<ctl(0) && get(1)<ctl(0)) || (get(0)>(ctl(0)-1)&&get(1)>(ctl(0)-1))?
(y%ctl(0))<(ctl(0)/2)?(y%ctl(0)+1)*(256*2/ctl(0)):(ctl(0)-y%ctl(0))*(256*2/ctl(0)):
(x%ctl(0))<(ctl(0)/2)?(x%ctl(0)+1)*(256*2/ctl(0)):(ctl(0)-x%ctl(0))*(256*2/ctl(0))
A: 255
ctl(0) Tile size
It works okay, the blend should not go as far to the center of each tile. So, wth another slider, we can control how deep the blend starts from the tile edge to the center, a fall-off control, you could say. That's why I left the 256*2/ctl(0) as is and did not change it into 512/ctl(0). The more I multiply, the faster I get values of 255 or above. The problem is, I have now three possible areas in a tile. It starts with a small black-white blend, stays white a while and finally a white-black blend. So the second code of the blend I have to check if I am in a non-blend area or in the white-black area. The reason I am doing this is for the ultimate filter, where the blends are combined with the image underneath, thus creating the weave pattern over an image. Let's check the vertical blend:
(y%ctl(0))<(ctl(0)/ctl(1))?(y%ctl(0)+1)*(256*ctl(1)/ctl(0)):(y%ctl(0)>(ctl(0)-1-ctl(0)/ctl(1)))?(ctl(0)-y%ctl(0))*(256*ctl(1)/ctl(0)):255
Slider 0 is the tile size and slider 1 is the brightness fall-off. The code before the ? checks if I am in the first boundary. If I am, the black-white blend is applied. If not, I check now if I am in the second boundary. If I am, the white-black blend is applied. If not, white (255) is applied. The whole code for this:
R:
put(x%(ctl(0)*2),0), put(y%(ctl(0)*2),1),
(get(0)<ctl(0) && get(1)<ctl(0)) || (get(0)>(ctl(0)-1)&&get(1)>(ctl(0)-1))?
(y%ctl(0))<(ctl(0)/ctl(1))?(y%ctl(0)+1)*(256*ctl(1)/ctl(0)):(y%ctl(0)>(ctl(0)-1-ctl(0)/ctl(1)))?(ctl(0)-y%ctl(0))*(256*ctl(1)/ctl(0)):255:
(x%ctl(0))<(ctl(0)/ctl(1))?(x%ctl(0)+1)*(256*ctl(1)/ctl(0)):(x%ctl(0)>(ctl(0)-1-ctl(0)/ctl(1)))?(ctl(0)-x%ctl(0))*(256*ctl(1)/ctl(0)):255
G,B:
(get(0)<ctl(0) && get(1)<ctl(0)) || (get(0)>(ctl(0)-1)&&get(1)>(ctl(0)-1))?
(y%ctl(0))<(ctl(0)/ctl(1))?(y%ctl(0)+1)*(256*ctl(1)/ctl(0)):(y%ctl(0)>(ctl(0)-1-ctl(0)/ctl(1)))?(ctl(0)-y%ctl(0))*(256*ctl(1)/ctl(0)):255:
(x%ctl(0))<(ctl(0)/ctl(1))?(x%ctl(0)+1)*(256*ctl(1)/ctl(0)):(x%ctl(0)>(ctl(0)-1-ctl(0)/ctl(1)))?(ctl(0)-x%ctl(0))*(256*ctl(1)/ctl(0)):255
A: 255
ctl(0) Tile size
ctl(1) Brightness
The following code changes the values returned by slider 1. I saw that slider values greater than 20 won't give much more effect, so I changed all ctl(1) into val(1,0,20).
R:
put(x%(ctl(0)*2),0), put(y%(ctl(0)*2),1),
(get(0)<ctl(0) && get(1)<ctl(0)) || (get(0)>(ctl(0)-1)&&get(1)>(ctl(0)-1))?
(y%ctl(0))<(ctl(0)/val(1,0,20))?(y%ctl(0)+1)*(256*val(1,0,20)/ctl(0)):
(y%ctl(0)>(ctl(0)-1-ctl(0)/val(1,0,20)))?(ctl(0)-y%ctl(0))*(256*val(1,0,20)/ctl(0)):255:
(x%ctl(0))<(ctl(0)/val(1,0,20))?(x%ctl(0)+1)*(256*val(1,0,20)/ctl(0)):
(x%ctl(0)>(ctl(0)-1-ctl(0)/val(1,0,20)))?(ctl(0)-x%ctl(0))*(256*val(1,0,20)/ctl(0)):255
G,B:
(get(0)<ctl(0) && get(1)<ctl(0)) || (get(0)>(ctl(0)-1)&&get(1)>(ctl(0)-1))?
(y%ctl(0))<(ctl(0)/val(1,0,20))?(y%ctl(0)+1)*(256*val(1,0,20)/ctl(0)):
(y%ctl(0)>(ctl(0)-1-ctl(0)/val(1,0,20)))?(ctl(0)-y%ctl(0))*(256*val(1,0,20)/ctl(0)):255:
(x%ctl(0))<(ctl(0)/val(1,0,20))?(x%ctl(0)+1)*(256*val(1,0,20)/ctl(0)):
(x%ctl(0)>(ctl(0)-1-ctl(0)/val(1,0,20)))?(ctl(0)-x%ctl(0))*(256*val(1,0,20)/ctl(0)):255
A: 255
ctl(0) Tile size
ctl(1) Brightness
The last step is to combine the pattern with the image with the multiply idea: c1*c2 / 256. I simply added the *c/256 to the blends and changed the 255 to c.
Category: Neology
Title: Digital weaver
Copyright: (c) 1997 by Werner D. Streidt
100526.16@compuserve.com
Author: Werner D. Streidt
Filename: ndigweav.8bf
R:
put(x%(ctl(0)*2),0), put(y%(ctl(0)*2),1),
(get(0)<ctl(0) && get(1)<ctl(0)) || (get(0)>(ctl(0)-1)&&get(1)>(ctl(0)-1))?
(y%ctl(0))<(ctl(0)/val(1,0,20))?(y%ctl(0)+1)*(256*val(1,0,20)/ctl(0))*c/256:
(y%ctl(0)>(ctl(0)-1-ctl(0)/val(1,0,20)))?(ctl(0)-y%ctl(0))*(256*val(1,0,20)/ctl(0))*c/256:c:
(x%ctl(0))<(ctl(0)/val(1,0,20))?(x%ctl(0)+1)*(256*val(1,0,20)/ctl(0))*c/256:
(x%ctl(0)>(ctl(0)-1-ctl(0)/val(1,0,20)))?(ctl(0)-x%ctl(0))*(256*val(1,0,20)/ctl(0))*c/256:c
G,B:
(get(0)<ctl(0) && get(1)<ctl(0)) || (get(0)>(ctl(0)-1)&&get(1)>(ctl(0)-1))?
(y%ctl(0))<(ctl(0)/val(1,0,20))?(y%ctl(0)+1)*(256*val(1,0,20)/ctl(0))*c/256:
(y%ctl(0)>(ctl(0)-1-ctl(0)/val(1,0,20)))?(ctl(0)-y%ctl(0))*(256*val(1,0,20)/ctl(0))*c/256:c:
(x%ctl(0))<(ctl(0)/val(1,0,20))?(x%ctl(0)+1)*(256*val(1,0,20)/ctl(0))*c/256:
(x%ctl(0)>(ctl(0)-1-ctl(0)/val(1,0,20)))?(ctl(0)-x%ctl(0))*(256*val(1,0,20)/ctl(0))*c/256:c
A: 255
ctl(0) Weave size
ctl(1) Shadow
a) A simple horizontal/vertical sine wave distortion
I know, there are some filters which would do the job in Photoshop (Ripple, Wave, Glass, Ocean ripple), but since this is a tutorial for people to learn to do effects, I'll put it in anyways. The objective is to put a (horizontal and a vertical) sine movement in the image (without wrapping).
To get information from neighbouring pixels we would need the src(x,y,z) function. The x and y values have to be changed with sinus values (sinus returns also negative values, remember?). The horizontal displacement (x) depends on its vertical position (y). Therefore we would have to use the basis src(x+sin(y),y,z). Let's say the cycle length is 4 pixels; y-pixels 0 to 3 have to return the values 0,512,0,-512. To convert this for our needs:
src(x + sin (y*1024/4), y, z)
Using the above code doesn't give nice results. Ok, now the amplitude: We have the possibility of getting values (according to our cycle length) between -512 and 512. Dividing the values by 512 would return us values between -1 and 1. Dividing the values by 256 would return us values between -2 and 2. This means we have to use smaller values in order to get greater amplitude values: sin(?)/(512/?) Our code would then look like this (with sliders as cycle lengths and amplitudes):
x + sin(y*1024/ctl(0)) / ( 512/ctl(2))
Now, for a complete filter:
Category: Neology
Title: Sinus-Waves
Copyright: (c) 1996 by Werner D. Streidt
100526.16@compuserve.com
Author: Werner D. Streidt
Filename: nsinwav.8bf
r,g,b: src(x + sin(y*1024/ctl(0)) / ( 512/ctl(2)),y + sin(x*1024/ctl(1))
/ ( 512/ctl(3)),z)
a: a
ctl(0) Horizontal cycle width (in pixels)
ctl(1) Vertical cycle width (in pixels)
ctl(2) Horizontal wave amplitude (in pixels)
ctl(3) Vertical wave amplitude (in pixels)
b) Doing the same with polar coordinates
In Photoshop, you can't do this effect :-). Actually, that is only half the truth. Indeed you have the zigzag filter with around center option. This makes kind of a sine wave along the angle lines witha certain amplitude (strength). With our filter, you can also make a sine wave around the center of the picture. I think I need not explain the why's and how's, because I simply changed src(x,y,z) with rad(d,m,z).
Category: Neology
Title: Polar-Waves
Copyright: (c) 1996 by Werner D. Streidt
100526.16@compuserve.com
Author: Werner D. Streidt
Filename: npolwav.8bf
r,g,b: rad(d+sin(m*1024/ctl(0))/(512/ctl(2)),m+sin(d*1024/ctl(1))/(512/ctl(3)),z)
a: a
ctl(0) Angle cycle width (in pixels)
ctl(1) Magnitude cycle width (in pixels)
ctl(2) Angle wave amplitude (in pixels)
ctl(3) Magnitude wave amplitude (in pixels)
TUTORIAL B: Offsetting the image (I) by Alfredo Mateus
Alf's Power Toys - A Filter Factory Tutorial
Channel Offset
Let's start with a very simple filter. All this filter does is displace your picture in the x or y direction, with sliders for each channel and each direction. You could do the exact same thing on the Offset filter in Photoshop. The big difference is that there you would have to go to the Channels palette and pick the channel you want to offset and repeat the filter three times, if you want to modify all three channels.
This filter is based on the src(x,y,z) function. The src function returns
the value for the pixel located in the (x,y) coordinates in the channel
z. For Photoshop (0,0) is located in the upper left corner of your picture.
Also, the R,G and B channels have z equal to 0, 1 and 2, respectively.
So, if you enter in FF:
src(0,0,z)
it will replace every pixel of your picture with the value of the first pixel. Try this out, zooming in the left corner of the picture and using the dropper and the info palette. So, if you enter src(x,y,z) this will not change the picture at all. For each pixel at position (x,y) it returns the value of itself. This is the same as using c in an expression.
What if I want the value of the neighbouring pixel? src(x+1,y,z) will displace the whole picture 1 pixel to the left. What happens when you get to the last pixel in a row, and you don't have a x+1 to get the value from (x is greater than the image's width)? In this case, the source pixel will equal the last available pixel (X-1). So src(x+10,y,z) will result in a streak of horizontal lines in the last 10 pixels. In this respect this is different from the Offset filter where you have the Wrap Around option.
In order to displace the image with slider values we would use:
src(x+ctl(0),y+ctl(1),z)
This will get the value of the slider 0 (ctl(0)) and displace the image to the left and the value of slider 1 (ctl(1)) and displace the picture upward. What if we want to go to the other direction?
src(x+((ctl(0)-128)*X/128),y+((ctl(1)-128)*Y/128),z)
When the slider is in the middle value (128), there is no displacement. Taking the slider to the right or left will cause displacement to opposite directions. We are multiplying with X/128, so that a maximum slider setting (0 or 255) returns us the fartherst (leftmost, rightmost) available pixels in our image. Another, more elegant way to do this is to use val instead of ctl:
src(x+val(0,-X,X)-1,y+val(1,-Y,Y)-1,z)
val takes the value of the slider and scales it between the two parameters, in this case the dimensions of the picture (X and Y).
All right, all we have to do now is place different sliders for each channel:
r: src(x+val(0,-X,X),y+val(1,-Y,Y),z)
g: src(x+val(2,-X,X),y+val(3,-Y,Y),z)
b: src(x+val(4,-X,X),y+val(5,-Y,Y),z)
a: a
The control names are:
ctl[0] = Red Horizontal
ctl[1] = Red Vertical
ctl[2] = Green Horizontal
ctl[3] = Green Vertical
ctl[4] = Blue Horizontal
ctl[5] = Blue Vertical
Now, as a homework, make the radial version of this filter using the rad function. You will get the Channel Spin filter.
As I said above, this filter will not wrap around the image. Let's see if we can get this into Filter Factory and we will have a very good Offset filter and maybe more.
The Wrapper (New Filter!)
This is my way to wrap an image. Mario has a filter to wrap an image completely in the middle (displacing half the dimensions in each direction). That was the Slipthrough filter. See also tutorial c for an equal filter. The Wrapper does it in an interactive way.
From the filter above we see that after displacing an image too much we get a portion of the image where it can't get info and so it repeats the edge pixel (which is one of the options in the Offset filter). This portion of the image is where we want to have the opposite end of the picture repeated. Let's see, if we displace the picture with src(x+val(0,0,X),y,z), the portion which gets the pixel repeated is given by X-val(0,0,X). Using the question mark we can select what filter factory will do in each area:
x<X-val(0,0,X)?src(x+val(0,0,X),y,z):src(x-(X-val(0,0,X)),y,z)
For x in the left of the repeated pixel area, it displaces the image just like before. For the repeated pixel area, it will place the info from the area that got bumped out to the left. We got wrapping! Let's try this for the vertical direction:
y<Y-val(1,0,Y)?src(x,y+val(1,0,Y),z):src(x,y-(Y-val(1,0,Y)),z)
Now, a little trick (I am pretty sure that Mario invented it) to get both in the same filter: the mode control.
ctl(2)<128?x<X-val(0,0,X)?src(x+val(0,0,X),y,z):
src(x-(X-val(0,0,X)),y,z):y<Y-val(0,0,Y)?src(x,y+val(0,0,Y),z):src(x,y-(Y-val(0,0,Y)),z)
ctl(2) is the mode control. If the slider is to the left of 128 it activates the horizontal wrapping. Greater than 128 we get vertical wrapping. I like both at the same time (which you can't get with the Offset filter (at least not without using two layers...). The final filter:
Name: The Wrapper
Category : Alf's Power Toys
Copyright: 1996 Alfredo Mateus
Author: Alfredo Mateus
r,g,b:
ctl(3)<85? x<X-val(0,0,X)?src(x+val(0,0,X),y,z):src(x-(X-val(0,0,X)),y,z)
:
ctl(3)<170? y<Y-val(1,0,Y)?src(x,y+val(1,0,Y),z):src(x,y-(Y-val(1,0,Y)),z)
:
mix(y<Y-val(1,0,Y)?src(x,y+val(1,0,Y),z):src(x,y-(Y-val(1,0,Y)),z),
x<X-val(0,0,X)?src(x+val(0,0,X),y,z):src(x-(X-val(0,0,X)),y,z),ctl(5),255)
a: a
ctl[0] = Horizontal Wrapping
ctl[1] = Vertical Wrapping
ctl[3] = Mode
ctl[5] = Mixing
I have tried the mixing of wrapping in both directions and if you have a tileable texture to start with, you'll get an interesting effect.
There are many other filters using the src function. This is but a very
small idea of what you can do with it. If you found this too simple, great,
you are past the beginer's level. You should be creating your own filters
soon! If you have any questions, send them to the list. Comments are welcome,
it may seem clear to me but completely weird to somebody else. FF codes
(normally more complex than these, like Mario's...) have a way to be impenetrable
sometimes...
TUTORIAL C: Offsetting the image (II)
Let's move our image around for a while. If we want to move our image 40 pixels to the right and 30 pixels downwards, we have to tell FF to put in the current pixel position the pixel value 40 pixels from the left and 30 over it:
src( x - 40, y - 30 , z)
In the coordinates between 0/0 and 39/29 FF will take the pixel values from 0/0 (because negative values are valued to 0 in FF) and repeat the edge pixels. But I'd like to wrap around. We have to first check the limits (in the following example for the x-coordinate):
(x < 40 ? X-39 +x: x-40 )
Is FF evaluating pixels 0 to 39, then it uses pixels from the right side of the image to wrap around. Is FF evaluating pixels in x-coordinates above 39, then it takes the pixel values from the pixel 40 pixels left (ok, read that again... :-)). Coding that for the y-coordinates, too will result to:
r,g,b: src(( x<40 ? X-39+x : x-40), (y<30 ? Y-29+y: y-30), z)
With slider 0 we control the horizontal movement, with slider 1 we control the vertical movement:
r,g,b: src(( x<ctl(0) ? X-ctl(0)+x: x-ctl(0) ), ( y<ctl(1) ? Y-ctl(1)+y: y-ctl(1) ), z)
What I'm getting at is the creation of a half wraparound for web images which are seamless. You would use this filter to wrap around the image and edit the edges for seamless tiling. We exchange the slider functions with X/2 and Y/2, respectively:
r,g,b: src(( x<X/2 ? X-X/2+x : x-X/2), (y<Y/2 ? Y-Y/2+y : y-Y/2), z)
X - X/2 gives X/2, so here's my Turnaround filter:
Category: Neology
Title: Turnaround
Copyright: (c) 1996 by Werner D. Streidt
100526.16@compuserve.com
Author: Werner D. Streidt
Filename: ntrnarnd.8bf
r,g,b: src(( x<X/2 ? X/2+x : x-X/2), (y<Y/2 ? Y/2+y : y-Y/2), z)
a: a
no sliders
Note: Use images with even width and length proportions. Even if you
can use the Photoshop internal offset filter, try both filters with on
selections. PS' offset filters knows negative image information, FF doesn't,
you may get interesting effects. A nice thing is that this works also
great on selections, FF only uses the selection info - Photoshop's Offset
Filter uses the whole image info. Try both filters with and without selections...
TUTORIAL D: Seamless tiling
The idea of the seamless tiling is to take part of the image, mirror it horizontally and vertically.
As an example:
r,g,b: src(x%100,y%100,z)
will fill your image with the 100 x 100 tile in the upper left of your image. If you want to change the width and height with sliders:
r,g,b: src(x%ctl(0), y%ctl(1),z)
ctl(0) tile width
ctl(1) tile height
You can change the idea of using always the upper left corner for tile data:
r,g,b: src(x%ctl(0)+ctl(2), y%ctl(1)+ctl(3),z)
ctl(0) tile width
ctl(1) tile height
ctl(2) horizontal offset
ctl(3) vertical offset
Now look what this baby does:
r,g,b: src(x%200<100?x%200:200-x%200-1,y%200<100?y%200:200-y%200-1,z)
It will take your 100 x 100 tile, mirror it sideways and mirror it downwards, thus creating a whole seamless tile pic.
And now with sliders for tile width, height and x/y offset:
Category: Neology
Title: Tiler1
Copyright: 1997 Werner D. Streidt http://www.fhd-stuttgart.de/~ws01
Author: Werner D. Streidt
Filename: ntiler1.8bf
r,g,b:
src(x%(ctl(0)*2)<ctl(0)?x%(ctl(0)*2)+ctl(2):(ctl(0)*2)-x%(ctl(0)*2)-1+ctl(2),
y%(ctl(1)*2)<ctl(1)?y%(ctl(1)*2)+ctl(3):(ctl(1)*2)-y%(ctl(1)*2)-1+ctl(3),z)
a: a
ctl(0): Tile width
ctl(1): Tile height
ctl(2): Horizontal offset
ctl(3): Vertical offset
Why does this happen and what can be done about it? The reason for this effect is, that FF scales down the original image for the preview and does all its the calculations for that preview with the measures of the small image you see in the window. That means that X is not 768 for example, but just 150 (this value varies from system to system). The problem occurs when you start moving around pixels. src(x-ctl(0),y,z) with ctl(0) set to 50 will shift the image 50 pixels to the right. In the preview this is almost 30% of the image, but in the final result, if you have an image that is 1000 pixels wide, it is just a small hop.
But there is of course a solution. You will have to scale the values of the sliders so they give you different results on the small and on the original image. Luckily this is pretty easy. Just replace the ctl(0) with val(0,0,X). That's it. If you fiddle around with y take val(0,0,Y) or val(0,-Y,Y) or val(0,40,5*Y) - as long as there is X,Y or M inside it will look right.
It gets a bit more complicated if it comes to the sin and cos functions. They will always return a result between -511 and 512 whatever you put in. So what I do is to convert their input in a way that I will always get a whole phase or a multiple of it. Therefore I use one of my favorite command:
The scl-function
I use this one in almost all of my filters because it is so comfortable. You put in a value that comes in a certain range and you'll receive something in a range that you need. Of course you could do that by adding and dividing, but in my opinion it is much easier and furthermore I don't trust the integer mathematics FF uses. If you divide something you'll always loose information as 5/3 in FF is 1 and not 1.6666. The scl command won't give you a different result, but somehow I hope the internal calculations are better that the external (probably not).
So what about this sin thing. We know that to get one sin phase we need to feed the function with the values from -511 to 511. x will never become negative and especially in the preview never get over 200.
Just for repetition here is the scl function as I read it:
scl([input value],[minimum expected input value],[maximum expected input value],[minimum output value], [maximum output value])
What we know is that x goes from 0 to X. Voilà, let's scale it: sin(scl(x,0,X,-511,512)).
if you want two phases, just multiply:
sin(2*scl(x,0,X,-511,512))
if you want to vary it use ctl()
sin(ctl(0)*scl(x,0,X,-511,512))
As you see you are allowed to use the normal ctl command here.
If you don't want the whole phase for some soft gradient for example you'll have to reduce the output of the scl function:
sin(scl(x,0,X,-254,255)) or sin(scl(x,0,X,-64,64))
As you see I prefer fractions of 2: 512, 256, 128, 64...
Oh I almost forgot. sin produces values from -511 to 512 but pixels accept only values from 0 to 255. Well, it's just another scale:
scl(sin(ctl(0)*scl(x,0,X,-511,512)),-511,512,0,255)
Yes of course (sin(ctl(0)*scl(x,0,X,-511,512))+511)/4 is the same, but scl is much easier to understand and easy to play around with it for experiments with variations of your final filter.
What do you do if you need a random value that works for a certain area of your image and not just on one pixel? Use the put command? Perhaps this would work, but you just have 256 possible variables that you can use. No, we have to create our own random function that works for all our needs. I just show you one way, but after you understood this you'll be able to create your own.
If there is enough code and stack space I prefer to use the tan funtion for that. It creates huge values what is important for us. The idea is to create a huge number and just take a part from it. To have a different value on every pixel we need to introduce something that changes with every pixel. There are some varaibles to choose from:
r g b i u v x y m d.
I wouldn't go for the color information as a black start image wouldn't produce very random results (but perhaps on some occasions it could be useful). I normally use x and y or, when working with radial filters m and d. The most basic random function would be tan(x*y) but as you see it is not good enough yet. Perhaps we should start tuning the output.
Let?s say we want RGB noise so we just need values from 0 to 255. Choose your weapons:
& or %: tan(x*y)&255 or tan(x*y)%255
Stop, % doesn't take care of the negative numbers so we need to add something:
abs(tan(x*y))%255
That looks better, but you can still see some repetitive patterns. That's where the huge number thing comes in:
(tan(x*y)*42)&255
Of course you can take any number you like. But there is still something missing. The upper and the leftmost line are not random enough. That's because either x or y are 0 there. No problem just add something:
(tan((x+1)*(y+1)*42)&255, better perhaps (tan((x+10)*(y+13))*42)&255
Again you are free to add whatever you like. In my eyes that's a pretty good noise, but we are not finished yet. Until now the noise is the same for every image, but perhaps you don't like it like this but prefer a little variation. Let's introduce a "Random Seed" slider:
(tan((x+10)*(y+13))*(42+ctl(7))&255
Here we are: our homemade random function. Feel free to add more variations:
(tan((5*x)*(y+13)*sin(x))*(42+ctl(7)))&255
(tan((5*x)*(y+13)*sin(cos(x)))*(42+ctl(7)))&255
But the best and most important thing is yet to come: The random function for areas that are bigger than 1 pixel. How about this:
(tan((5*x%val(0,0,X))*(y%val(1,0,Y)+13)*sin(x%val(0,0,X)))*(42+ctl(7)))&255
(tan((5*x%val(0,0,X))*(y%val(1,0,Y)+13)*sin(cos(x%val(0,0,X))))*(42+ctl(7)))&255
If something works with x and y it also works with m and d. All you have to do is to replace every x with m, every y with d and the same with X and Y (on the sliders for example). Sometimes it is necessary to use d+511 or abs(d) instead of a simple d, as d produces negative values. Also you have to watch out that the scaling of d is different to that of Y. scl(y,0,255,1234,43525) would become scl(d,-512,512,1234,43525). If you have a very big filter this doesn't work sometimes as m and d need more internal stack space and you'll just see the ! sign even if the code has no errors. In this case try to use as few m and d as possible by using put(m,0),put(d,1) in the beginning,
A texture can be a fine displacement map. If you have created a nice texture generator, especially one with smooth gradients you can make a distortion filter out of it. Let's say you have a beautiful function that produces shades between 0 and 255 (that's what texture generators normally do). What we need is just a grayscale version of it. Put the result into an empty variable:
put([fantastic code],9)
Now comes the distortion thing:
src(x,y-scl(get(9),0,255,-val(7,0,Y),val(7,0,Y)),z)
If you want to have control over the horizontal distortion, too try this:
src(x-scl(get(9),0,255,-val(6,0,X),val(6,0,X)),y-scl(get(9),0,255,-val(7,0,Y),val(7,0,Y)),z)
But you can spice up the look even more by introducing some shading. You already have the shades in get(9) all you have to do is to merge it with the src results. Depending on how much stack space you have left there are different methods. One of the easiest (but not best) is to simply add the shades:
src(x,y-scl(get(9),0,255,-val(7,0,Y),val(7,0,Y)),z)+get(9)-128
Watch that I subtracted 128 to correct the brightness. To get just the shadows I use the classic multiply method:
src(x,y-scl(get(9),0,255,-val(7,0,Y),val(7,0,Y)),z)*get(9)/256
For just the highlights I take the screen mode:
255-(255-src(x,y-scl(get(9),0,255,-val(7,0,Y),val(7,0,Y)),z))*(255-get(9))/256
My current favorite is an average of both. But as it is pretty long this doesn't work if the rest of your code uses already lots of stack space. As I have to do 2 calculations I save the src result in a variable:
put(src(x,y-scl(get(9),0,255,-val(7,0,Y),val(7,0,Y)),z),10), ((get(9)*get(10)/256)+(255-(255-get(9))*(255-get(10))/256))/2
If something works on the whole image it also works on small tiles. At least for filters that use x and y (for m and d it's a bit more complicated). Actually you just put the following code on the beginning:
put(val(7,0,min(X,Y)),0),put(x%get(0),1),put(y%get(0),2)
Now replace every x in your filter with get(1), every y with get(2) and every X or Y with get(0). If you want to control the height and the width of the tiles individually the code loks like this:
put(val(6,0,X),0),put(val(7,0,Y),1),put(x%get(0),2),put(y%get(1),3)
Accordingly x becomes get(2), y becomes get(3), X becomes get(0) and Y becomes get(1).
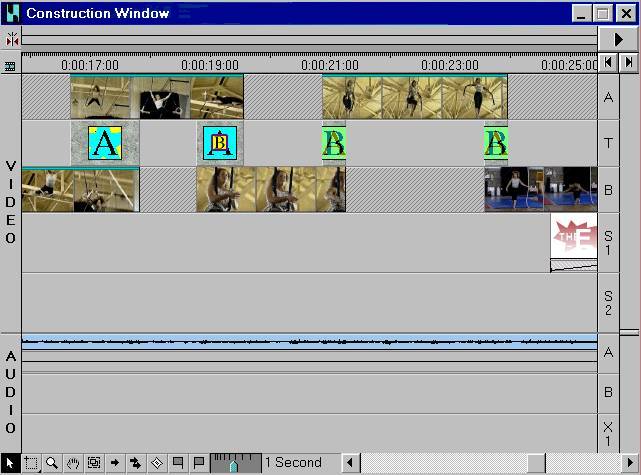
The first track of the Construction Window, the A-Track, is intended for the first video sequence, the second is the T-Track where the Transitions are placed and the third, the B-Track, is for the video sequence that follows. Below them there are up to 99 S-Tracks where titles oder other videos can be placed for overlaying the videos on Track A and B. Last but not least there are up to 99 Audio-Tracks for placing the sound of Video A und B and mixing them with background music. (Premiere can also be used for multitrack sound mixing, although it doesn't offer the comfort of Samplitude Studio, Cubase VST, Cool Edit Pro etc.)
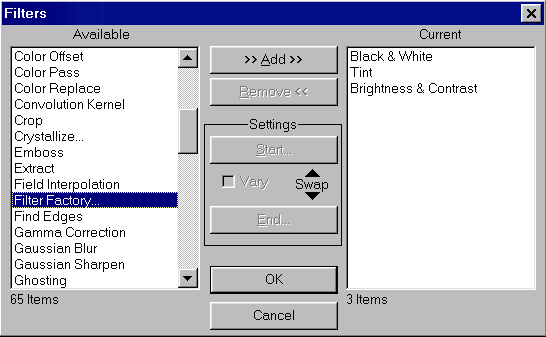
Filters are applied to a video, picture, title etc. by holding down the right mouse button above a video sequence and selecting "Filters ...". The Filters window pops up then, where you can select the available filters from a list box. Besides the display in a list box, a major difference to Photoshop is that you can apply several filters at the same time, so that the result of the first filter is used as input for the second etc. .
In the Settings frame there is another great feature ot Premiere: you can simulate a filter with changing results without using the t and total expressions in the filter code (see 3.3.1!). Firstly you have to add a filter and define the start values of the sliders, then by activateing the Vary check box the plugIn dialog will appear again, but now you have to set the end values. By using "Start..." and "End..." you can redefine those slider values.
Assuming that you set the start value of Slider One to 20 and the end
value to 200, the start value of Slider Two to 0 and the end value to
255 and have a video containing ten frames, Premiere will automatically
change the slider values when processing the video in the following way
:
| Frame | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Changing value of Slider 1 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 |
| Changing value of Slider 2 | 0 | 28 | 56 | 84 | 112 | 140 | 168 | 204 | 232 | 255 |

Transitions are placed in the T-Track , as mentioned above, and adjusted in their length and position. You can apply a Transition to a single video which is almost the same as using a filter, but you can adjust what part of a video sequence is manipulated (See Section 3.5.2 !). Usually a Transition is applied between the beginning and the end of 2 videos, so that a transition from one scene to the other is created.
A major difference is that Premiere's FF calculates the channel the otherway round compared to Photoshop's FF. The blue channel is calculated first, then the green one, then the red channel. It is very strange that the interface of Premiere's FF doesn't reflect this!
Furthermore, there are many differences concerning the programming code between both Filter Factories. Here are the most important ones (This list will be updated in future!):
c-val(a,b,c)
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 9 | 8 | 7 |
| 6 | 5 | 4 |
| 3 | 2 | 1 |
No explaination needed.
Look at 3.3
I think some great filters could be done in this way.
Even more greater effects could be achived this way! Imagine 2 videos melting and seperating.
Look at the Transition Factory Tutorial.
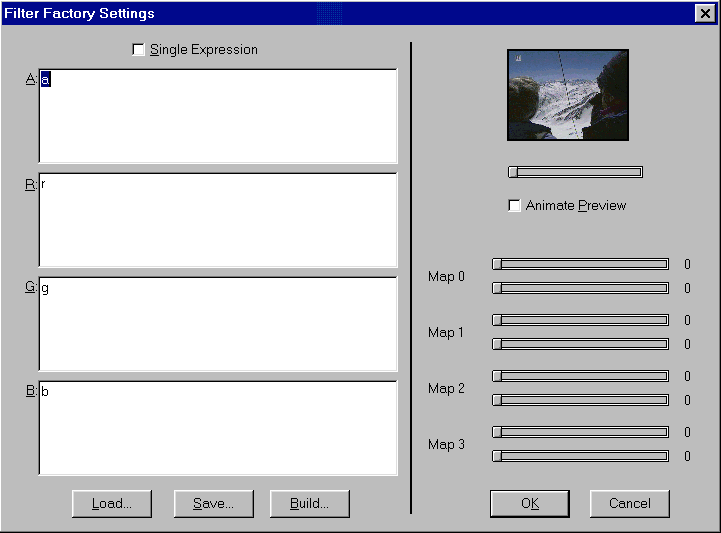
As in Photoshop's Filter Factory there are four text fields for entering the filter code, as well as a preview and 8 Sliders above it. The Buttons "Load", "Save" and "Build" have also the same functions as in Photoshop. New is the slider under the preview and the checkbotton Animate Preview. By dragging the slider you can see the result of the filter on every frame of a video and by activating the checkbox the video is played to show the effect of your code continously. When activating the checkbox "Single Expression" three of four code fields disappear. The code entered in the remaining field is used on all four channels (R, G, B, A).
To compile your filter you have to press "Build". The following window will pop up:

In this window you can enter the file name of the compiled .prm file (Premiere PlugIn), the name that will appear in the Filter dialogbox and a note about the author and copyright. Below it you can select which sliders or maps are to be displayed in the compiled filter.
Transition Factory is used almost exactly as Filter Factory. The Transition Factory has to be dragged from the Transitions window to the T-Track to make the Transition Factory Settings window appear. Further differences are that you can enter a description of the transition in the Build window and that it is placed in the Transitions window showing a preview of its effect (as you can see in the third picture above!).
Here's a visualisation how it works (total = 10):
| Frame | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Dissolve percent (t/total) |
10% (1/10) |
20% (2/10) |
30% (3/10) |
40% (4/10) |
50% (5/10) |
60% (6/10) |
70% (7/10) |
80% (8/10) |
90% (9/10) |
100% 1 |
3.7.1.2 Iris Round
The second transition will be more complicated. It simulates an opening
or closing cirlce that reveals Video B.
Iris Round Open:
Iris Round Close:
G, R: get(0)?c0:c1
Iris Sqare Close:
G, R: get(0)?c0:c1
Iris Square Open:
G, R: get(0)?c1:c0
G, R: ctl(0)<128?get(0)?c0:c1:get(0)?c1:c0
Iris Cross:
G, R: get(2)? c1:c0
To have the reverse effect we just have to replace t with (total-t) and turn>= into <= (or swap c0 and c1).
Radial Wipe from bootm left corner to top left corner:
G, R: get(1)?c0:c1
G, R: get(0)? c1:c0
Horizontal Slide from left to right:
Horizontal Slide from right to left:
Would you like to create a one big from those four formulas? I prefer to create two transitions instead:
Horizontal Slide:
G, R : get(0)?src1(get(1),y,p):c0
G, R : get(0)?src1(x,get(1),p):c0
Horizontal Push from left to right:
To get a vertical push just replace x and X wit y and Y.
To keep the calculation time low, you should create for each of the 4 formulas a own plugin.
Vertikal Barn Doors to the borders:
Vertikal Closing Split:
G, R: x<get(0)?src1(get(1),y,p): (X-x)<=get(0)? src1(get(2),y,p):c0
Horizontal Closing Split:
G, R: y<get(0)?src1(x,get(1),p): (Y-Y)<=get(0)? src1(x,get(2),p):c0
Horizontal Opening Split:
G, R: y<get(0)?src0(x,get(1),p): (Y-y)<=get(0)?src0(x,get(2),p):c1
G, R: get(0) && get(1)? c0:c1
G, R: t<=T/2?src0(get(1),get(2),p):src1(get(1),get(2),p)
3.7.2.1 "Halftime" Transitions
Haftime transitions are transitions that do something with video 0 in the first half of the transition and manipulate video 1 in the second half. Such transitions always begin with the expression t<=total/2?
G, R: t<=T/2?c0-get(0):c1-get(1)
Inverse Flash:
G, R: t<=(T/2)?x>get(0)? src0(get(0),y,p):c0: x<get(1)? c1:src1(get(1),y,p)
Vertical Stream:
G, R: t<=(T/2)?y>get(0)? src0(x,get(0),p):c0: y<get(1)?c1:src1(x,get(1),p)
3.7.2.2 "Fulltime" Transitions
Fulltime Transitions are transitions that manipulate video 0 and video 1 continuesly. You have already seen some examples in 3.7.1 Simulating program solutions.
If you have any questions about this FAQ (you don't understand a tutorial in here or flame me because of a spelling error), feel free to contact me:
Werner D. Streidt 100526.16@compuserve.com
or the author mentioned in the tutorial.
Adobe Photoshop and Adobe Premiere are trademarks of Adobe Systems, Inc. All rights reserved.
Althought free downloadable, no part of the contents of this document may be reproduced in any form or by any means without written permission of the author. The authors of this document have used their best efforts in creating it. However, the author makes no warranties of any kind, express or implied, with regard to the documentation or filter codes contained. In no event shall the author be responsible or liable of any loss of profit or any commercial damages in connection with the use of this document or filter codes.